---

---

Fecha: 31/1/2021. Por: David Luna

---

• El repositorio con el código fuente completo está aquí

Sudoku y su complejidad

Sudoku es un gran juego para jugar solo, y también excelente para resolver de manera programática. El juego tiene reglas sencillas, pero logra ofrecer un reto. Las reglas son las siguientes:

1. Hay una cuadrícula de 9x9 con celdas que pueden ser llenadas con números del 1 al 9.
2. Los números no pueden ser repetidos en el mismo renglón o columna.
3. Cada subcuadrícula de 3x3 no puede tener números repetidos.

Un ejemplo de una cuadrícula inicial es el siguiente:

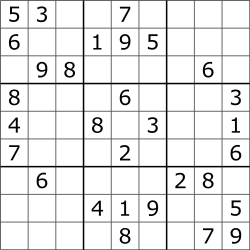
(Imagen tomada del artíuclo de Sudoku de Wikipedia

La solución más simplre sería usar un método de fuerza bruta para llenar las celdas vacías de la cuadrícula, pero esto no sería óptimo y tomaría un largo tiempo con las versiones más difíciles del juego que tienen menos celdas llenas al principio. Considerando que hay un total de 81 celdas y cada una de ellas puede tener un número del 1 al 9, se puede asumir que la complejidad en el peor de los casos es de O(81^9). Si bien el número de celdas vacias al principio es menor que 81, intentar rellenar el resto solamente con fuerza bruta sigue siendo un problema, ya que lleva a muchas soluciones que no son correctas o ni siquiera tienen sentido.

Hay ciertos pasos que pueden ser tomados para evitar esto:

1. Revisar que si se rompe alguna regla al asignar el valor de alguna celda para no expandir el árbol de manera innecesaria.
2. Hacer backtracking si una regla no es respetada, ya que esta solución a partir de este punto no es correcta.
3. Limitar los valores possibles para cada celda, con el fin de reducir el dominio y complejidad del problema.

Sudoku y los problemas de satisfacción de restricciones

Los problemas de satisfacción de restricciones (CSPs por sus siglas en inglés) son problemas cuyos estados deben cumplir un conjunto de restricciones para ser considerados válidos. De cierto modo, los pasos mencionados anteriormente son exactamente esto, un modo de establecer restricciones que se deben cumplir para que una cuadrícula de Sudoku tenga sentido y no rompa las reglas. Cuando se define un CSP, es importante determinar las variables del problema, su dominio y las restricciones del problema. En el caso de este puzle, los datos son los siguientes:

• El conjunto de variables que representan cada celda de la cuadrícula de 9x9 es: X = {X1, X2, ..., X81}.
• El dominio de cada variable es el conjunto de números del 1 al 9: D = {1,2,3,4,5,6,7,8,9}.
• Las restricciones son las reglas mencionadas anteriormente: dos variables no pueden tener el mismo valor si están en el mismo renglón, columna o subcuadrícula de 3x3.

Una vez que el problema es modelado como un CSP, se pueden tomar diferentes acercamientos para resolverlo. En este caso, para definir Sudoku como un CSP las siguientes estructuras de datos son requeridas:

using VarType = Loc;
using VarValType = int;

class Loc {
  public:
	uint8_t row, col;
	Loc(uint8_t x, uint8_t y);
};

bool operator<(const Loc &loc1, const Loc &loc2);
bool operator==(const Loc &loc1, const Loc &loc2);

class CSP {
  public:
	std::map<VarType, std::set<VarValType>> domains;
	std::map<VarType, std::vector<VarType>> arcs;

	CSP();
	void printCSP(bool prettyPrint);
	void doBacktracking();
	void readCSP();

  private:
	std::vector<VarType> sortedVars; // For use in the backtracking solution

	bool isVarConsistent(const VarType &var);
	void buildArcs(const VarType &var);
	bool solutionHelper(unsigned long depth);
};

Nota: el uso de los operadores < y == para la clase Loc es necesario para usar la clase como llave al usar map y set. La implementación puede ser vista aquí .

La clase Loc sirve para guardas las coordenadas (x,y) de cada celda de la cuadrícula de 9x9. CSP tiene los siguientes miembros:

• domains define el conjunto de valores que cada celda puede tomar.
• arcs define qué celdas tienen restricciones entre sí.

El constructor CSP define los arcos de cada celda de la cuadrícula. Recorre cada posición y llama al método buildArcs. La función invocada agrega al conjunto de vecinos de loc a cada variable en la misma columna, renglón y subcuadrícula de 3x3.

const uint8_t nRows = 9;
const uint8_t nCols = 9;
const uint8_t sSize = 3;

CSP::CSP() {
	for (uint8_t i = 0; i < nRows; ++i) {
		for (uint8_t j = 0; j < nCols; ++j) {
			Loc tempLoc(i, j);
			arcs.insert(std::make_pair(tempLoc, std::vector<Loc>{}));
			buildArcs(tempLoc);
		}
	}
}

void CSP::buildArcs(const Loc &loc) {
	for (uint8_t i = 0; i < nRows; ++i) {
		if (i != loc.row) {
			arcs.find(loc)->second.push_back(Loc(i, loc.col));
		}
	}
	for (uint8_t j = 0; j < nCols; ++j) {
		if (j != loc.col) {
			arcs.find(loc)->second.push_back(Loc(loc.row, j));
		}
	}
	uint8_t sRow = loc.row / sSize;
	uint8_t sCol = loc.col / sSize;
	for (uint8_t i = sRow * sSize; i < (sRow + 1) * sSize; ++i) {
		if (i != loc.row) {
			for (uint8_t j = sCol * sSize; j < (sCol + 1) * sSize; ++j) {
				if (j != loc.col) {
					arcs.find(loc)->second.push_back(Loc(i, j));
				}
			}
		}
	}
}

El algoritmo AC-3

El algoritmo AC-3 es un algoritmo the sirve para reducir el dominio de las variables estableciendo la consistencia del arco de cada restricción. El algoritmo revisa cada restricción entre los pares de variables (x,y) y elimina los valores de los dominios de x y y que no cumplen dichas restricciones. En este caso, el algoritmo es útil para reducir los posibles valores de cada celda de {1,2...,9} a sólo aquellos que no rompan las reglas.

Con el CSP definido, el algoritmo AC-3 utiliza dos funciones para reducir los dominios de las variables y asegurar que las restricciones son cumplidas.

• ac3Algorithm: esta función crea una cola que almacena todos los pares de variables (x,y), los cuales representan cada una de las restricciones del problema. Después, entra en un ciclo que llama a la función removeInconsistencies con cada par en la cola. Si la función regresa true, todos los vecinos de x son insertados en la cola como el siguiente tipo de par (vecino, x). El ciclo termina cuando la cola de pares ha sido procesada por completo.
• removeInconsistencies: esta función recive loc1 y loc2, que representan a x y y de ac3Algorithm respectivamente. Revisa si los valores del dominio de loc1 cumplen con la restricción con loc2. Con el puzle de sudoku la restricción sería incumplida si el dominio de loc2 es de tamaño 1 y su único valor está en el dominio de loc1. Como el dominio de loc2 no puede estar vacío, el valor es eliminado del dominio de loc1. Si no se detecta algún incumplimiento de las restricciones del problema, la función regresa false o true en caso contrario.

bool removeInconsistencies(CSP &sudo, Loc loc1, Loc loc2) {
	std::set<int> *currSet = &sudo.domains.find(loc2)->second;
	for (auto curr : sudo.domains.find(loc1)->second) {
		if (currSet->size() == 1 && currSet->count(curr)) {
			sudo.domains.find(loc1)->second.erase(curr);
			return true;
		}
	}
	return false;
}

void ac3Algorithm(CSP &csp) {
	std::queue<std::pair<Loc, Loc>> arcQueue;
	for (auto cell : csp.arcs) {
		auto loc = cell.first;
		if (csp.domains.find(loc)->second.size() > 1) {
			for (auto neighbor : cell.second) {
				arcQueue.push(std::make_pair(loc, neighbor));
			}
		}
	}

	while (!arcQueue.empty()) {
		std::pair<Loc, Loc> curr = arcQueue.front();
		arcQueue.pop();
		if (removeInconsistencies(csp, curr.first, curr.second)) {
			for (auto neighbor : csp.arcs.find(curr.first)->second) {
				arcQueue.push(std::make_pair(neighbor, curr.first));
			}
		}
	}
}

Backtracking y la heurística de menor cantidad de valores restantes

Ahora que el dominio de cada variable ha sido reducido para cumplir con las restricciones del problema, el siguiente paso es aplicar backtracking (vuelta atrás en español) para resolverlo. Cabe mencionar que en algunos casos el uso del algoritmo AC-3 basta para resolver el problema, mas no siempre, y menos con las versiones más difíciles.

Una heurística útil para usar junto al backtracking es la heurística de menor cantidad de valores restantes. Al usar esta técnica, los nodos con los dominios más pequeños son explorados primero, dejando las variables con dominios grandes para ser exploradas hasta el final. Si se detecta un incumplimiento de las restricciones al hacer backtracking, una cantidad grande de ramas son eliminadas y dejan de ser consideradas para expandir, ahorrando así el esfuerzo computacional de explorar soluciones no válidas.

Para aplicar esta heurística las variables con un dominio mayor a uno son organizadas de acuerdo al tamaño de su dominio. El vector sortedVars se usa para llevar el control de qué variables tienen los dominios más pequeños. La llamada a la función std::sort con la ayuda de la función para comparar locComp se encarga de este paso. Después, la función recursiva auxiliar es llamada para empezar el proceso de backtracking.

void CSP::doBacktracking() {
	auto locComp = [this](const Loc &loc1, const Loc &loc2) {
		return domains.find(loc1)->second.size() < domains.find(loc2)->second.size();
	};

	for (auto loc : domains) {
		sortedVars.push_back(loc.first);
	}
	std::sort(sortedVars.begin(), sortedVars.end(), locComp);
	solutionHelper(0);
}

La función solutionHelper es una función recursiva que recive la produndidad o índice del vector sortedVars. Selecciona la variable loc de dicho índice y la usa para establecer su dominio. Los pasos que sigue son los siguientes:

1. Si la produndidad o índice recibido es mayor o igual al tamaño de sortedVars, regresa true.
2. Selecciona la variable loc y crea un conjunto temporal para almacenar el dominio actual de dicha variable.
3. Toma el valor var y lo vuelve el único en el dominio de loc, eliminándolo al mismo tiempo de las variables vecinas que tienen alguna restricción con loc.
4. Si no hay inconsistencias, es decir que no hay vecinos con dominios vacíos y la llamada recursiva a solutionHelper regresa verdadero, regresa true.
5. Si el paso anterior falló, regresa el var al dominio de las variables vecinas de loc.
6. Si no hay valores en el dominio original de loc que permitan ser asignados sin incurrir en un incumplimiento de las restricciones, regresa false.

bool CSP::solutionHelper(unsigned long depth) {
	if (depth >= sortedVars.size()) {
		return true;
	}
	const Loc *loc = &sortedVars.at(depth);
	std::set<int> domain = domains.find(*loc)->second;
	for (int var : domain) {
		domains.find(*loc)->second = std::set<int>{var};
		std::vector<bool> wasErased;
		for (auto neighbor : arcs.find(*loc)->second) {
			auto *neighborDomain = &domains.find(neighbor)->second;
			if (neighborDomain->count(var)) {
				neighborDomain->erase(var);
				wasErased.push_back(true);
			} else {
				wasErased.push_back(false);
			}
		}
		if (isVarConsistent(*loc) && solutionHelper(depth + 1)) {
			return true;
		}
		int i = 0;
		for (auto neighbor : arcs.find(*loc)->second) {
			if (wasErased.at(i++)) {
				domains.find(neighbor)->second.insert(var);
			}
		}
	}
	domains.find(*loc)->second = domain;
	return false;
}

Momento de juntar las piezas

El único paso restante es definir las funciones readCSP y printCSP. Para readCSP el código es el siguiente:

std::set<int> initialDomain = {1, 2, 3, 4, 5, 6, 7, 8, 9};

void CSP::readCSP() {
	for (uint8_t i = 0; i < numRows; ++i) {
		std::string temp;
		std::cin >> temp;
		for (unsigned long int j = 0; j < temp.size(); ++j) {
			uint8_t curr = temp.at(j) - '0';
			if (curr) {
				domains.insert(std::make_pair(Loc(i, j), std::set<int>{curr}));
			} else {
				domains.insert(std::make_pair(Loc(i, j), initialDomain));
			}
		}
	}
}

Imprimir el CSP es cuestión de iterar sobre domains e imprimir el dominio de cada celda de la cuadrícula. La implementación se encuentra aquí

Con todo esto implementado, la manera de juntar todo es tan sencillo como el siguiente fragmento de código:

int main() {
	CSP csp;

	csp.readCSP();
	ac3Algorithm(csp);
	csp.doBacktracking();
	std::cout << "Output:\n";
	csp.printCSP(true);

	return 0;
}